Some results on neural networks

Test on JAZ


std error train: 2.19 std error test: 2.32
max error train: 5.54 max error test: 5.54
std error train: 0.67 std error test: 0.71
max error train: 2.04 max error test: 2.01

This is the result after 100 training epochs
In [7]: testthresholds()
 0.00 <#:  395> <EUR:    4.57> <EUR/trade: 0.012> <%: 77.09> <%/trade:  0.20>
 0.05 <#:  346> <EUR:    4.69> <EUR/trade: 0.014> <%: 79.25> <%/trade:  0.23>
 0.10 <#:  301> <EUR:    5.11> <EUR/trade: 0.017> <%: 82.02> <%/trade:  0.27>
 0.15 <#:  258> <EUR:    5.34> <EUR/trade: 0.021> <%: 86.22> <%/trade:  0.33>
 0.20 <#:  208> <EUR:    4.97> <EUR/trade: 0.024> <%: 76.80> <%/trade:  0.37>
 0.25 <#:  152> <EUR:    4.72> <EUR/trade: 0.031> <%: 74.67> <%/trade:  0.49>
 0.30 <#:  129> <EUR:    4.27> <EUR/trade: 0.033> <%: 68.26> <%/trade:  0.53>
 0.35 <#:  101> <EUR:    3.61> <EUR/trade: 0.036> <%: 59.96> <%/trade:  0.59>
 0.40 <#:   83> <EUR:    3.22> <EUR/trade: 0.039> <%: 53.38> <%/trade:  0.64>
 0.45 <#:   62> <EUR:    2.43> <EUR/trade: 0.039> <%: 43.28> <%/trade:  0.70>
 0.50 <#:   55> <EUR:    2.39> <EUR/trade: 0.043> <%: 42.46> <%/trade:  0.77>
 0.55 <#:   51> <EUR:    2.28> <EUR/trade: 0.045> <%: 40.74> <%/trade:  0.80>
 0.60 <#:   45> <EUR:    1.78> <EUR/trade: 0.040> <%: 32.21> <%/trade:  0.72>
 0.65 <#:   38> <EUR:    1.34> <EUR/trade: 0.035> <%: 24.70> <%/trade:  0.65>
 0.70 <#:   34> <EUR:    1.39> <EUR/trade: 0.041> <%: 25.23> <%/trade:  0.74>
 0.75 <#:   25> <EUR:    0.83> <EUR/trade: 0.033> <%: 14.28> <%/trade:  0.57>
 0.80 <#:   20> <EUR:    0.58> <EUR/trade: 0.029> <%:  9.79> <%/trade:  0.49>
 0.85 <#:   10> <EUR:    0.65> <EUR/trade: 0.065> <%: 11.84> <%/trade:  1.18>
 0.90 <#:    8> <EUR:    0.51> <EUR/trade: 0.064> <%:  9.66> <%/trade:  1.21>
 0.95 <#:    4> <EUR:    0.37> <EUR/trade: 0.092> <%:  7.17> <%/trade:  1.79>
 1.00 <#:    3> <EUR:    0.33> <EUR/trade: 0.109> <%:  6.47> <%/trade:  2.16>

In [8]: able2generalize(buildsignals(0.6))
For NEW signals
   gain>0.sum()  --winning sum 0.292  # 3
   gain<0.sum()  --loosing sum -0.236  # 3
   gain/loss ratio :  1.23728813559  Hit ratio :  1.0
For OLD signals
   gain>0.sum()  --winning sum 2.538  # 27
   gain<0.sum()  --loosing sum -0.811  # 12
   gain/loss ratio :  3.12946979038  Hit ratio :  2.25

In [9]: able2generalize(buildsignals(0.7))
For NEW signals
   gain>0.sum()  --winning sum 0.292  # 3
   gain<0.sum()  --loosing sum -0.079  # 1
   gain/loss ratio :  3.69620253165  Hit ratio :  3.0
For OLD signals
   gain>0.sum()  --winning sum 1.825  # 21
   gain<0.sum()  --loosing sum -0.646  # 9
   gain/loss ratio :  2.82507739938  Hit ratio :  2.33333333333

In [10]: able2generalize(buildsignals(0.8))
For NEW signals
   gain>0.sum()  --winning sum 0.227  # 1
   gain<0.sum()  --loosing sum -0.079  # 1
   gain/loss ratio :  2.87341772152  Hit ratio :  1.0
For OLD signals
   gain>0.sum()  --winning sum 0.961  # 12
   gain<0.sum()  --loosing sum -0.526  # 6
   gain/loss ratio :  1.82699619772  Hit ratio :  2.0

After some more training (100+)

In [13]: testthresholds()
 0.00 <#:  395> <EUR:    7.54> <EUR/trade: 0.019> <%:118.29> <%/trade:  0.30>
 0.05 <#:  325> <EUR:    7.25> <EUR/trade: 0.022> <%:118.08> <%/trade:  0.36>
 0.10 <#:  281> <EUR:    7.12> <EUR/trade: 0.025> <%:117.50> <%/trade:  0.42>
 0.15 <#:  250> <EUR:    7.06> <EUR/trade: 0.028> <%:117.26> <%/trade:  0.47>
 0.20 <#:  218> <EUR:    5.50> <EUR/trade: 0.025> <%: 93.98> <%/trade:  0.43>
 0.25 <#:  192> <EUR:    5.63> <EUR/trade: 0.029> <%: 95.48> <%/trade:  0.50>
 0.30 <#:  165> <EUR:    5.35> <EUR/trade: 0.032> <%: 90.27> <%/trade:  0.55>
 0.35 <#:  140> <EUR:    5.05> <EUR/trade: 0.036> <%: 86.64> <%/trade:  0.62>
 0.40 <#:  120> <EUR:    4.60> <EUR/trade: 0.038> <%: 78.43> <%/trade:  0.65>
 0.45 <#:  101> <EUR:    4.65> <EUR/trade: 0.046> <%: 78.80> <%/trade:  0.78>
 0.50 <#:   83> <EUR:    4.08> <EUR/trade: 0.049> <%: 69.27> <%/trade:  0.83>
 0.55 <#:   71> <EUR:    4.02> <EUR/trade: 0.057> <%: 69.81> <%/trade:  0.98>
 0.60 <#:   63> <EUR:    3.22> <EUR/trade: 0.051> <%: 59.43> <%/trade:  0.94>
 0.65 <#:   58> <EUR:    2.98> <EUR/trade: 0.051> <%: 55.46> <%/trade:  0.96>
 0.70 <#:   52> <EUR:    2.76> <EUR/trade: 0.053> <%: 51.10> <%/trade:  0.98>
 0.75 <#:   47> <EUR:    2.53> <EUR/trade: 0.054> <%: 47.97> <%/trade:  1.02>
 0.80 <#:   42> <EUR:    2.14> <EUR/trade: 0.051> <%: 39.21> <%/trade:  0.93>
 0.85 <#:   35> <EUR:    1.50> <EUR/trade: 0.043> <%: 28.33> <%/trade:  0.81>
 0.90 <#:   26> <EUR:    0.60> <EUR/trade: 0.023> <%: 11.54> <%/trade:  0.44>
 0.95 <#:   22> <EUR:    0.68> <EUR/trade: 0.031> <%: 11.80> <%/trade:  0.54>
 1.00 <#:   18> <EUR:    0.65> <EUR/trade: 0.036> <%: 11.09> <%/trade:  0.62>

In [14]: able2generalize(buildsignals(0.6))
For NEW signals
   gain>0.sum()  --winning sum 0.58  # 8
   gain<0.sum()  --loosing sum -0.329  # 4
   gain/loss ratio :  1.76291793313  Hit ratio :  2.0
For OLD signals
   gain>0.sum()  --winning sum 4.025  # 37
   gain<0.sum()  --loosing sum -1.052  # 14
   gain/loss ratio :  3.82604562738  Hit ratio :  2.64285714286

In [15]: able2generalize(buildsignals(0.7))
For NEW signals
   gain>0.sum()  --winning sum 0.462  # 6
   gain<0.sum()  --loosing sum -0.329  # 4
   gain/loss ratio :  1.40425531915  Hit ratio :  1.5
For OLD signals
   gain>0.sum()  --winning sum 3.424  # 31
   gain<0.sum()  --loosing sum -0.797  # 11
   gain/loss ratio :  4.29611041405  Hit ratio :  2.81818181818

In [16]: able2generalize(buildsignals(0.8))
For NEW signals
   gain>0.sum()  --winning sum 0.462  # 6
   gain<0.sum()  --loosing sum -0.293  # 3
   gain/loss ratio :  1.57679180887  Hit ratio :  2.0
For OLD signals
   gain>0.sum()  --winning sum 2.516  # 25
   gain<0.sum()  --loosing sum -0.54  # 8
   gain/loss ratio :  4.65925925926  Hit ratio :  3.125


If targets are set to +/-0.8 instead of +/-1, many less signals are generated, although with more profit per trade:
In [33]: testthresholds()
 0.00 <#:  395> <EUR:    3.57> <EUR/trade: 0.009> <%: 68.60> <%/trade:  0.17>
 0.05 <#:  337> <EUR:    2.63> <EUR/trade: 0.008> <%: 52.00> <%/trade:  0.15>
 0.10 <#:  209> <EUR:    3.55> <EUR/trade: 0.017> <%: 61.01> <%/trade:  0.29>
 0.15 <#:  125> <EUR:    4.09> <EUR/trade: 0.033> <%: 71.54> <%/trade:  0.57>
 0.20 <#:   73> <EUR:    3.98> <EUR/trade: 0.055> <%: 68.25> <%/trade:  0.93>
 0.25 <#:   36> <EUR:    2.85> <EUR/trade: 0.079> <%: 48.34> <%/trade:  1.34>
 0.30 <#:   24> <EUR:    2.32> <EUR/trade: 0.097> <%: 37.38> <%/trade:  1.56>
 0.35 <#:   19> <EUR:    1.79> <EUR/trade: 0.094> <%: 29.80> <%/trade:  1.57>
 0.40 <#:   13> <EUR:    1.27> <EUR/trade: 0.097> <%: 20.72> <%/trade:  1.59>
 0.45 <#:   10> <EUR:    1.16> <EUR/trade: 0.116> <%: 19.55> <%/trade:  1.96>
 0.50 <#:   10> <EUR:    1.16> <EUR/trade: 0.116> <%: 19.55> <%/trade:  1.96>
 0.55 <#:    9> <EUR:    1.17> <EUR/trade: 0.130> <%: 19.81> <%/trade:  2.20>
 0.60 <#:    8> <EUR:    0.97> <EUR/trade: 0.122> <%: 15.51> <%/trade:  1.94>
 0.65 <#:    7> <EUR:    0.88> <EUR/trade: 0.126> <%: 13.86> <%/trade:  1.98>
 0.70 <#:    6> <EUR:    0.84> <EUR/trade: 0.140> <%: 13.33> <%/trade:  2.22>
 0.75 <#:    5> <EUR:    0.71> <EUR/trade: 0.142> <%: 11.16> <%/trade:  2.23>
 0.80 <#:    4> <EUR:    0.27> <EUR/trade: 0.068> <%:  6.09> <%/trade:  1.52>
 0.85 <#:    4> <EUR:    0.27> <EUR/trade: 0.068> <%:  6.09> <%/trade:  1.52>
 0.90 <#:    3> <EUR:    0.11> <EUR/trade: 0.038> <%:  3.05> <%/trade:  1.02>
 0.95 <#:    3> <EUR:    0.11> <EUR/trade: 0.038> <%:  3.05> <%/trade:  1.02>
 1.00 <#:    3> <EUR:    0.11> <EUR/trade: 0.038> <%:  3.05> <%/trade:  1.02>

A neural network to predict the next value of a sine wave

Reportedly, neural networks are able to learn complex rules. Let's see if they can learn to predict the next value of a sine wave...

Predicting from two past values

Start generating pairs of values of a sine wave described by cos(6t) and a sampling period of 0.1s

t=t=np.linspace(0,10,101)
ds = SupervisedDataSet(2, 1)
s1=np.cos(6*t)

for ix in range(2,101):
   ds.addSample(s1[ix-2:ix],s1[ix])

Then, build the neural network

net = buildNetwork(2, 3, 1, hiddenclass=TanhLayer) 
trainer = BackpropTrainer(net, ds)



Make a different dataset for testing. Note it has the same frequency

# Test dataset with different values
dst = SupervisedDataSet(2, 1)
st=np.cos(6*(t-0.11))
for ix in range (2,101):
   dst.addSample(st[ix-2:ix],st[ix])

Define a function to test quality of the resulting network

def evalnet():
  
   out=net.activateOnDataset(dst)
   stderr=np.std(out.T-st[2:101])
   print 'std error :'+str(stderr)

Then train the network and display result repeatedly:

trainer.trainEpochs(200)
evalnet()

Here are the results

Run #1
In [81]: execfile( 'example_sine.py')
std error :0.475135957881
std error :0.00528582169261
std error :0.00420217821467
std error :0.00388770773851

Run #2
In [82]: execfile( 'example_sine.py')
std error :0.825420526812
std error :0.0231771366421
std error :0.0206355959287
std error :0.0188795980662

Run #2
In [83]: execfile( 'example_sine.py')
std error :0.790629966353
std error :0.0095095475289
std error :0.0078286464515
std error :0.00764017583539

Is the network able to predict cos(5t) if trained for cos(6t)?

In [88]: execfile( 'example_sine.py')
std error :0.981991629948
std error :0.0691771695798
std error :0.0695395180253
std error :0.0691409803733

In [89]: execfile( 'example_sine.py')
std error :1.20686164247
std error :0.0741454399328
std error :0.0724747717285
std error :0.0700249455395

So, it doesn't perform very well, but it is fair enough!

If we set up a dataset with 50% of data corresponding to cos(5t) and 50% corresponding to cos(6t) and test with a similar data set:

In [123]: execfile( 'example_sine.py')
std error :0.513686241649
std error :0.0340440621768
std error :0.0339060173516
std error :0.0338778895194

In [125]: execfile( 'example_sine.py')
std error :0.669916052193
std error :0.0395873020069
std error :0.0374792495802
std error :0.0359768805783

In [126]: execfile( 'example_sine.py')
std error :0.696332858547
std error :0.037025395267
std error :0.0363592341024
std error :0.03641336896

How well does it predict a sine wave of a different amplitude?

tt=np.linspace(0,0.2,3)
In [153]: v=0.5*np.cos(5*tt-4); print v;net.activate([v[0],v[1]])
[-0.32682181 -0.46822834 -0.49499625]
Out[153]: array([-0.58104487])

Not quite well but, again, fair enough!

What happens with a network with more hidden neurons? 2,3,1 -> 2,5,1

In [156]: execfile( 'example_sine.py')
std error :1.04554148959
std error :0.0385415333149
std error :0.0388701113238
std error :0.0386260279819  <- similar to before

In [157]: v=0.5*np.cos(5*tt-4); print v;net.activate([v[0],v[1]])
[-0.32682181 -0.46822834 -0.49499625]
Out[157]: array([-0.48321326])

And with another hidden layer? 2,3,1 -> 2,3,3,1

In [161]: execfile( 'example_sine.py')
std error :0.788084537967
std error :0.0435729774591
std error :0.041549014995
std error :0.0398895692455

In [162]: v=0.2*np.cos(5*tt-2); print v;net.activate([v[0],v[1]])
[-0.08322937  0.01414744  0.10806046]
Out[162]: array([ 0.00811018])

With 2,3,1 -> 2,4,4,1 it performs more or less the same

Predicting from three past values

In [203]: execfile( 'example_sine3.py')
std error :0.849241666555
max error :2.67855045373
std error :0.0536682726789
max error :0.120103597074
std error :0.0475902319921
max error :0.108592376129
std error :0.0422407920624
max error :0.0944045487712

In [204]: v=0.7*np.cos(5.5*tt-0.2); print v;net.activate([v[0],v[1],v[2]])
[ 0.6860466   0.6575609   0.43512698  0.08435194]
Out[204]: array([ 0.07766859])

In [205]: v=0.5*np.cos(4*tt-0.2); print v;net.activate([v[0],v[1],v[2]])
[ 0.49003329  0.49003329  0.41266781  0.27015115]
Out[205]: array([ 0.21284467])

In [206]: v=0.6*np.cos(4.2*tt-0.6); print v;net.activate([v[0],v[1],v[2]])
[ 0.49520137  0.59030622  0.58280278  0.47399534]
Out[206]: array([ 0.41496148])
Works very good!

Neural networks for stock market prediction

Tools which I have chosen: pyBrain

There is also neuroph, which seems an instructive tool written in java. This link has also an interesting tutorial on predicting a sine wave.

To install pyBrain:

sudo apt-get install python-setuptools

sudo easy_install pybrain

A Losing Strategy?

A given strategy gives you x1.2 your original investment 50% of the time and x0.822 your original investment 50% of the time.Note that 1.2·0.822 = 0.98623 which is less than one. So, if you trade this system 100 times with your full equity, assuming you get 50 winning and 50 losing trades, your will end up with a 50% loss, as 1.2^50*0.822^50=0.5.

This is not appealing, is it? But, what happens if you always trade a fraction "f" of your current equity? Look a the graph below, showing the simulated results for 10k experiments:

As in this post, the blue shaded areas correspond to areas including 25%, (darkest), 50%, 75% and 90% (lightest) of the outcomes. The frontiers between areas are 5%, 12.5%, 25%, 37.5%, 62.5%, 75%, 87.5% and 90% percentiles. The solid blue line corresponds to the theoretical case: half of the results lie above and half below this line. The green line is the mean of the outcomes.

It follows, that you may get a final equity E, greater than the initial one Eo. Specifically E>1.016·Eo in 62.5% of the cases if you make each trade with f=0.1, i.e. 10% of our equity.

The following simulation is a similar case where the gains are x1.5 and x0.6575:

Clearly, this might be attractive, depending on your level of risk!

What quantity should I trade?

Problem Outline

Let's suppose you have developed a trading system. On average, 50% of the trades give you a 10% profit and 50% of the trades give you a 5% loss. 

The Theory

Suppose that you have an initial account of 100 and you make 50 trades. In each trade you invest your total equity. In theory, 25 trades would increase your equity by a factor 1.1, and 25 trades would decrease it by a factor 0.95. So, the net result should be

E  =  Eo·1.1^25·0.95^25  =  Eo·3

So, your final equity would be 3 times your initial equity Eo.

What happens if you invest a fraction f (0<f<1) of your equity in each trade? On each trade you take f away and you recover f*1.1 or f*0.95. Assuming 25 successful and 25 unsuccessful trades, you end up with

E(f)  =  Eo·(1-f+f*1.1)^25 ·(1-f+f*0.95)^25

Simulation of Real Cases

What happens in practice? I have made some simulations of trading sequences. Random numbers between 0 and 1 are generated. If they are > 0.5, we assume a gain of 1.1, else a loss of 0.95.  Figure 1 shows the resulting equity after 50 trades for different values of f.

Figure 1

The green line is the theory discussed above, the blue line is the mean of 1000 experiments. There is a reasonable agreement. In addition, the plot shows a filled area, which corresponds to the mean plus minus one standard deviation. The dashed green lines correspond to the theoretical case, but with 55% gains and 45% losses and vice-versa.

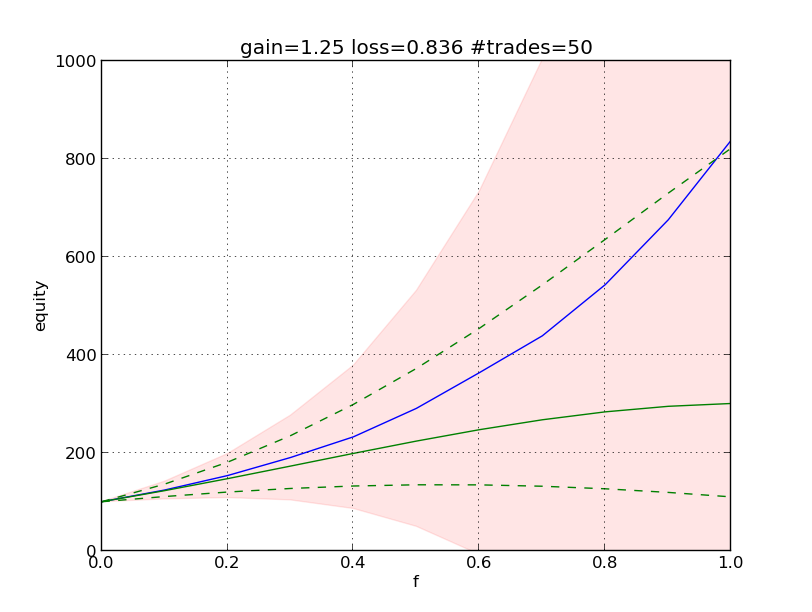
What happens if we change the gain (pg) and loss (pl) levels? Figure 2 shows the results of a simulation for pg=1.25, pl=0.836 for 50 trades. To get a smoother curve, this has been done for 10k experiments.

Figure 2

The green line is, again, the theory. Trading the full account (f=1) this gives the same theoretical result E=Eo·3 as before. The green curve is, however quite flat, suggesting that, we may trade smaller amounts with similar result.

Observe the green dashed lines, obtained as before. If a specific run has 55% losses, instead of 50%, and we are trading with f=1, we will end up with E=Eo·1.1.

It seems also surprising that the blue line, the mean of 10k experiments, looks so much "better" than the theory. This may be explained because there is a lower limit of 0.836^50, i.e. 0 for practical purposes and an upper limit of >70000. Note that we have a distribution that is not normal (in the statistical sense).

The coloured area may be misleading, suggesting negative outcomes. Keep in mind that it is only a representation of the standard deviation of the blue line. For f=1 the mean is 838 and the standard deviation is 2167!

More meaningful results are obtained from the plot in Figure 3. Here, I have added blue dotted lines corresponding to the percentiles 5%, 15%, 25% 50%, 75%, 85% and 95%.

Figure 3. Blue dotted lines at 5%, 15%, 25% 50%, 

75%, 85% and 95% percentiles

We may observe that the percentile 50% line falls exactly on the green (theoretical) line. We also observe that there is roughly a 20% chance that we end up losing money (E<100) with this technique when f=1.

Some interesting conclusions:

• If we want to trade with this technique and we want be sure that we do NOT lose money in 95% of the cases, we should NOT trade. This is indicated by the maximum of the lowest dotted line being at f=0
• If we want to maximize our return in 75% of the cases, we should invest at the maximum of the third dotted line, which happens at f=0.65 

Discussion

1) The simulation of real cases (there is some irony in this!) shows that reality is quite different from the theory. The case discussed in the first chapter of The Mathematics of Money Management by Ralph Vince, showing a nice and sharp maximum for f=0.25, only happens for games with extreme gain (and loss) values, which we are unlikely to find in trading.

2) The results are very sensitive if gains and losses are big and small, respectivelly. To achieve a theoretical final value E=Eo·3 for pg=1.5, we need

pl=3^(1/25)/1.5=0.69662

But, if we use two decimal positions and compute 1.5^25·0.69^25 we get E=Eo·2.34, and 1.5^25·0.69^25 gives E=Eo·3.38

3) Mean and standard deviation are useless measures if the distribution is not normal. Percentiles give more information. In our case, the theoretical case corresponds to the 50% percentile.

Some "Equivalent" Systems

Next are the simulation plots for some systems with pg·pl=1, which are theoretically equivalent if traded with f=1: they all give E=Eo after 100 trades. There are, however significant differences between them!

 Figure 4

 Figure 5

Figure 6

In these plots, the blue shaded areas correspond to areas including 25%, (darkest), 50%, 75% and 90% (lightest) of outcomes. The frontiers between areas are 5%, 12.5%, 25%, 37.5%, 62.5%, 75%, 87.5% and 90% percentiles. The solid blue line corresponds to the theoretical case: half of the results lie above and half below this line. The green line is the mean of the outcomes. The long tails of the resulting distribution are responsible for the upward bias, but this is nevertheless, the real mean!

So, if you were offered one of these three systems, what would you do? You could elect the first one, where pg=1.3 and pl=0.77. Trading using this system with f=0.3 you will obtain E>1.25·Eo in 75% of the occasions. Do NOT trade this system with f=1!

Getting stock data

Some sites, like megabolsa, give end of day stock quotes.

You may download each file with
wget http://www.megabolsa.com/cierres/140102.txt

The information is in the following format


SYMB,DATE(yyyymmdd),APE, MAX,MIN,CLOSE,VOL

For this kind of files to be processed, a newline character has to be appended at the file end. This is achieved with

echo >> 140102.txt

To convert the comma separated file to a "|"separated file and change the data format from yyymmdd to yyyy-mm-dd, use

awk -F',' '{x=$2;yy=substr(x,1,4);mm=substr(x,5,2); dd=substr(x,7,2); $2=yy"-"mm"-"dd}1' OFS='|' 140102.txt > tmpfile.txt
Explanation:

1. find a comma -F','
2. date is in the second field x=$2
3. get the substrings mm=substr(x,5,2)
4. compose result $2=yy"-"mm"-"dd
5. return 1 (?) and make the output file separator a pipe character '|'

We can do this for all our files, sort them, and send them to the same output file (make sure it does not exist before)

awk -F',' '{x=$2;yy=substr(x,1,4);mm=substr(x,5,2);dd=substr(x,7,2); $2=yy"-"mm"-"dd}1' OFS='|' 2014_diarios/*.txt | sort >>tmp.txt

Finally, do the same processing as in this post. First, insert empty columns to comply with the beancounter structure:

awk -F'|' '{$(NF)="0|0|0" FS $(NF);}1' OFS='|' tmp.txt | awk -F'|' '{$(3)="0" FS $(3);}1' OFS='|' > tmp.txt.cut
And then, insert into the database
sqlite3 val.db
sqlite> .import tmp.txt.cut stockprices



PD: You may join all of your files with cat
cat *.txt |sort > out.txt

Useful links

• TA-Lib Python wrapper for TA-Lib (http://ta-lib.org/). The documentation has interesting pointers to the original sources.
• A python example to start playing.
• Ultra-Finance  Python project for real-time financial data collection, analyzing && backtesting trading strategies
• Retrieve Yahoo quotes. Basic module
• Pandas example to retrieve Yahoo quotes

• High Frequency Trading acceleration using FPGAs   By Christian Leber, Benjamin Geib, Heiner Litz
• Finantial Information Exchange  (FIX) Introduction to the data format used
• API calls to brokers. Open Source request
• QuickFIX Open Source FIX implementation

• Quantstart. Web page for quantitative trading. Link to free resources
• quantifiedstrategies Automatic trading. Test of some strategies. Very interesting tests an track records.
• Trading with Python   
• Algorithmic Trading with Free Open Source Software   
• AuTraSyBlog    Automated Trading System
  Systematic Trading research and development, with a flavour of Trend Following
  
  

  • Stock Market prediction using neural networks.

Convert Metastock data to mySQL

Metastock is a well-known stock analysis program with a proprietary data format. Some web pages, for instance megabolsa, provide historical data in metastock format. To be able to make our own tools, we will need a better format. The tool mySQL is a reasonable source for this. It is widely available everywhere.

To extract the metastock information, atem is a useful tool which can be downloaded from here.

Next we illustrate the procedure to load the metastock data stored in directory hist for a given stock (spanish Tubacex in this example) to a mySQL database:

Display help for atem64
./atem64 --help

List the different ticker symbols in the directory
./atem64 --symbols --field-separator=,  ../hist

./atem64 --symbols --field-separator=,  ../hist | grep TUB
Produces this output: TUB,Tubacex,D,1986-02-14,2013-12-31,89,F89.DAT,63,156,M

This is useful to locate the file for tubacex: F89.DAT

./atem64 --fdat=89  --field-separator=,  ../hist
Print on screen the CSV file corresponding to TUB

Generate tub.txt file with a | separator
Remove time information for end-of-day data. Change date-from as needed.
./atem64 --fdat=89  --field-separator='|'  --date-from=2013-01-01 --format=-time hist |grep TUB > tub.txt

Some raw processing of the generated file:

1.Cut the last column from tub.txt
2.Insert 0 for day_change, bid, ask before volume information
3.Insert 0 for previous close, after date and before open

cut -d'|' -f -7 tub.txt | awk -F'|' '{$(NF)="0|0|0" FS $(NF);}1' OFS='|' | awk -F'|' '{$(3)="0" FS $(3);}1' OFS='|' > tub.txt.cut

Finally,create the table with this
rm val.db
sqlite3 val.db < createtable.sql
sqlite> .import tub.txt.cut stockprices

where createtable.sql has the following content:

CREATE TABLE stockprices (
        symbol          varchar(12) not null default '',
        date            date default null,
        previous_close  real default null,
        day_open        real default null,
        day_high        real default null,
        day_low         real default null,
        day_close       real default null,
        day_change      real default null,
        bid             real default null,
        ask             real default null,
        volume          numeric default null
    );
CREATE UNIQUE INDEX stockprices_pkey
        on stockprices (symbol, date);

This table should be compatible with the beancounter format.