A Losing Strategy?

A given strategy gives you x1.2 your original investment 50% of the time and x0.822 your original investment 50% of the time.Note that 1.2·0.822 = 0.98623 which is less than one. So, if you trade this system 100 times with your full equity, assuming you get 50 winning and 50 losing trades, your will end up with a 50% loss, as 1.2^50*0.822^50=0.5.

This is not appealing, is it? But, what happens if you always trade a fraction "f" of your current equity? Look a the graph below, showing the simulated results for 10k experiments:

As in this post, the blue shaded areas correspond to areas including 25%, (darkest), 50%, 75% and 90% (lightest) of the outcomes. The frontiers between areas are 5%, 12.5%, 25%, 37.5%, 62.5%, 75%, 87.5% and 90% percentiles. The solid blue line corresponds to the theoretical case: half of the results lie above and half below this line. The green line is the mean of the outcomes.

It follows, that you may get a final equity E, greater than the initial one Eo. Specifically E>1.016·Eo in 62.5% of the cases if you make each trade with f=0.1, i.e. 10% of our equity.

The following simulation is a similar case where the gains are x1.5 and x0.6575:

Clearly, this might be attractive, depending on your level of risk!

What quantity should I trade?

Problem Outline

Let's suppose you have developed a trading system. On average, 50% of the trades give you a 10% profit and 50% of the trades give you a 5% loss. 

The Theory

Suppose that you have an initial account of 100 and you make 50 trades. In each trade you invest your total equity. In theory, 25 trades would increase your equity by a factor 1.1, and 25 trades would decrease it by a factor 0.95. So, the net result should be

E  =  Eo·1.1^25·0.95^25  =  Eo·3

So, your final equity would be 3 times your initial equity Eo.

What happens if you invest a fraction f (0<f<1) of your equity in each trade? On each trade you take f away and you recover f*1.1 or f*0.95. Assuming 25 successful and 25 unsuccessful trades, you end up with

E(f)  =  Eo·(1-f+f*1.1)^25 ·(1-f+f*0.95)^25

Simulation of Real Cases

What happens in practice? I have made some simulations of trading sequences. Random numbers between 0 and 1 are generated. If they are > 0.5, we assume a gain of 1.1, else a loss of 0.95.  Figure 1 shows the resulting equity after 50 trades for different values of f.

Figure 1

The green line is the theory discussed above, the blue line is the mean of 1000 experiments. There is a reasonable agreement. In addition, the plot shows a filled area, which corresponds to the mean plus minus one standard deviation. The dashed green lines correspond to the theoretical case, but with 55% gains and 45% losses and vice-versa.

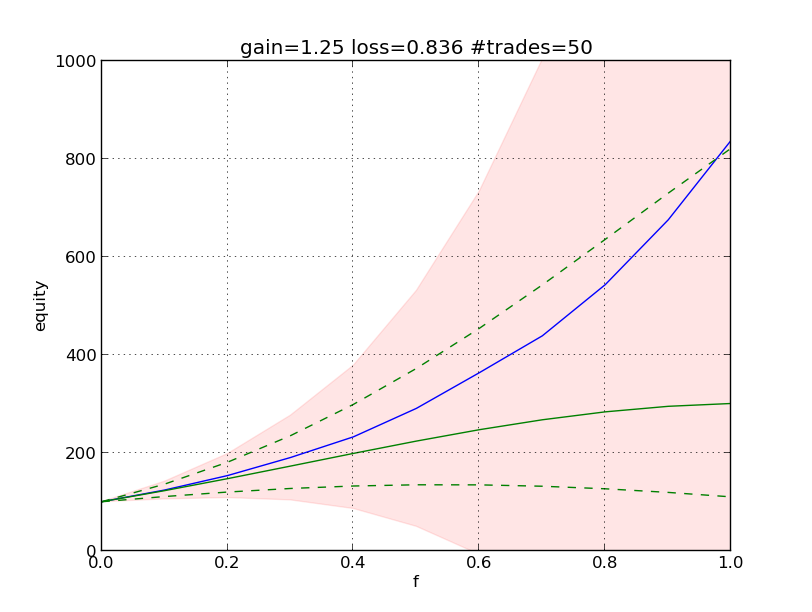
What happens if we change the gain (pg) and loss (pl) levels? Figure 2 shows the results of a simulation for pg=1.25, pl=0.836 for 50 trades. To get a smoother curve, this has been done for 10k experiments.

Figure 2

The green line is, again, the theory. Trading the full account (f=1) this gives the same theoretical result E=Eo·3 as before. The green curve is, however quite flat, suggesting that, we may trade smaller amounts with similar result.

Observe the green dashed lines, obtained as before. If a specific run has 55% losses, instead of 50%, and we are trading with f=1, we will end up with E=Eo·1.1.

It seems also surprising that the blue line, the mean of 10k experiments, looks so much "better" than the theory. This may be explained because there is a lower limit of 0.836^50, i.e. 0 for practical purposes and an upper limit of >70000. Note that we have a distribution that is not normal (in the statistical sense).

The coloured area may be misleading, suggesting negative outcomes. Keep in mind that it is only a representation of the standard deviation of the blue line. For f=1 the mean is 838 and the standard deviation is 2167!

More meaningful results are obtained from the plot in Figure 3. Here, I have added blue dotted lines corresponding to the percentiles 5%, 15%, 25% 50%, 75%, 85% and 95%.

Figure 3. Blue dotted lines at 5%, 15%, 25% 50%, 

75%, 85% and 95% percentiles

We may observe that the percentile 50% line falls exactly on the green (theoretical) line. We also observe that there is roughly a 20% chance that we end up losing money (E<100) with this technique when f=1.

Some interesting conclusions:

• If we want to trade with this technique and we want be sure that we do NOT lose money in 95% of the cases, we should NOT trade. This is indicated by the maximum of the lowest dotted line being at f=0
• If we want to maximize our return in 75% of the cases, we should invest at the maximum of the third dotted line, which happens at f=0.65 

Discussion

1) The simulation of real cases (there is some irony in this!) shows that reality is quite different from the theory. The case discussed in the first chapter of The Mathematics of Money Management by Ralph Vince, showing a nice and sharp maximum for f=0.25, only happens for games with extreme gain (and loss) values, which we are unlikely to find in trading.

2) The results are very sensitive if gains and losses are big and small, respectivelly. To achieve a theoretical final value E=Eo·3 for pg=1.5, we need

pl=3^(1/25)/1.5=0.69662

But, if we use two decimal positions and compute 1.5^25·0.69^25 we get E=Eo·2.34, and 1.5^25·0.69^25 gives E=Eo·3.38

3) Mean and standard deviation are useless measures if the distribution is not normal. Percentiles give more information. In our case, the theoretical case corresponds to the 50% percentile.

Some "Equivalent" Systems

Next are the simulation plots for some systems with pg·pl=1, which are theoretically equivalent if traded with f=1: they all give E=Eo after 100 trades. There are, however significant differences between them!

 Figure 4

 Figure 5

Figure 6

In these plots, the blue shaded areas correspond to areas including 25%, (darkest), 50%, 75% and 90% (lightest) of outcomes. The frontiers between areas are 5%, 12.5%, 25%, 37.5%, 62.5%, 75%, 87.5% and 90% percentiles. The solid blue line corresponds to the theoretical case: half of the results lie above and half below this line. The green line is the mean of the outcomes. The long tails of the resulting distribution are responsible for the upward bias, but this is nevertheless, the real mean!

So, if you were offered one of these three systems, what would you do? You could elect the first one, where pg=1.3 and pl=0.77. Trading using this system with f=0.3 you will obtain E>1.25·Eo in 75% of the occasions. Do NOT trade this system with f=1!

Getting stock data

Some sites, like megabolsa, give end of day stock quotes.

You may download each file with
wget http://www.megabolsa.com/cierres/140102.txt

The information is in the following format


SYMB,DATE(yyyymmdd),APE, MAX,MIN,CLOSE,VOL

For this kind of files to be processed, a newline character has to be appended at the file end. This is achieved with

echo >> 140102.txt

To convert the comma separated file to a "|"separated file and change the data format from yyymmdd to yyyy-mm-dd, use

awk -F',' '{x=$2;yy=substr(x,1,4);mm=substr(x,5,2); dd=substr(x,7,2); $2=yy"-"mm"-"dd}1' OFS='|' 140102.txt > tmpfile.txt
Explanation:

1. find a comma -F','
2. date is in the second field x=$2
3. get the substrings mm=substr(x,5,2)
4. compose result $2=yy"-"mm"-"dd
5. return 1 (?) and make the output file separator a pipe character '|'

We can do this for all our files, sort them, and send them to the same output file (make sure it does not exist before)

awk -F',' '{x=$2;yy=substr(x,1,4);mm=substr(x,5,2);dd=substr(x,7,2); $2=yy"-"mm"-"dd}1' OFS='|' 2014_diarios/*.txt | sort >>tmp.txt

Finally, do the same processing as in this post. First, insert empty columns to comply with the beancounter structure:

awk -F'|' '{$(NF)="0|0|0" FS $(NF);}1' OFS='|' tmp.txt | awk -F'|' '{$(3)="0" FS $(3);}1' OFS='|' > tmp.txt.cut
And then, insert into the database
sqlite3 val.db
sqlite> .import tmp.txt.cut stockprices



PD: You may join all of your files with cat
cat *.txt |sort > out.txt

Useful links

• TA-Lib Python wrapper for TA-Lib (http://ta-lib.org/). The documentation has interesting pointers to the original sources.
• A python example to start playing.
• Ultra-Finance  Python project for real-time financial data collection, analyzing && backtesting trading strategies
• Retrieve Yahoo quotes. Basic module
• Pandas example to retrieve Yahoo quotes

• High Frequency Trading acceleration using FPGAs   By Christian Leber, Benjamin Geib, Heiner Litz
• Finantial Information Exchange  (FIX) Introduction to the data format used
• API calls to brokers. Open Source request
• QuickFIX Open Source FIX implementation

• Quantstart. Web page for quantitative trading. Link to free resources
• quantifiedstrategies Automatic trading. Test of some strategies. Very interesting tests an track records.
• Trading with Python   
• Algorithmic Trading with Free Open Source Software   
• AuTraSyBlog    Automated Trading System
  Systematic Trading research and development, with a flavour of Trend Following
  
  

  • Stock Market prediction using neural networks.

Convert Metastock data to mySQL

Metastock is a well-known stock analysis program with a proprietary data format. Some web pages, for instance megabolsa, provide historical data in metastock format. To be able to make our own tools, we will need a better format. The tool mySQL is a reasonable source for this. It is widely available everywhere.

To extract the metastock information, atem is a useful tool which can be downloaded from here.

Next we illustrate the procedure to load the metastock data stored in directory hist for a given stock (spanish Tubacex in this example) to a mySQL database:

Display help for atem64
./atem64 --help

List the different ticker symbols in the directory
./atem64 --symbols --field-separator=,  ../hist

./atem64 --symbols --field-separator=,  ../hist | grep TUB
Produces this output: TUB,Tubacex,D,1986-02-14,2013-12-31,89,F89.DAT,63,156,M

This is useful to locate the file for tubacex: F89.DAT

./atem64 --fdat=89  --field-separator=,  ../hist
Print on screen the CSV file corresponding to TUB

Generate tub.txt file with a | separator
Remove time information for end-of-day data. Change date-from as needed.
./atem64 --fdat=89  --field-separator='|'  --date-from=2013-01-01 --format=-time hist |grep TUB > tub.txt

Some raw processing of the generated file:

1.Cut the last column from tub.txt
2.Insert 0 for day_change, bid, ask before volume information
3.Insert 0 for previous close, after date and before open

cut -d'|' -f -7 tub.txt | awk -F'|' '{$(NF)="0|0|0" FS $(NF);}1' OFS='|' | awk -F'|' '{$(3)="0" FS $(3);}1' OFS='|' > tub.txt.cut

Finally,create the table with this
rm val.db
sqlite3 val.db < createtable.sql
sqlite> .import tub.txt.cut stockprices

where createtable.sql has the following content:

CREATE TABLE stockprices (
        symbol          varchar(12) not null default '',
        date            date default null,
        previous_close  real default null,
        day_open        real default null,
        day_high        real default null,
        day_low         real default null,
        day_close       real default null,
        day_change      real default null,
        bid             real default null,
        ask             real default null,
        volume          numeric default null
    );
CREATE UNIQUE INDEX stockprices_pkey
        on stockprices (symbol, date);

This table should be compatible with the beancounter format.